Finite Impulse Response (FIR) filters (pronounced either “F-I-R” or alternately, like the tree) are the rage these days.
Like many things in audio, they have been around a very long time, but technology has now evolved to allow their practical implementation. Is this the panacea that we have been waiting for, the “filter messiah” that will finally allow perfect sound reproduction?
Of course not, but they are pretty cool nonetheless, and they can be a game changer for some applications.
This is part 1 of a series that will examine the use of FIR filters in sound reinforcement systems. There are plenty of textbooks and resources on the Internet that delve into the mathematics and the deep theory.
That’s a bottomless well that can never be exhausted. In this series I’ll use a broad brush stroke to give some “take-aways” on FIR filter theory along with practical implementations and examples. These will hopefully prove beneficial for understanding FIRs and integrating FIR filter technology into your projects.
I will assume an understanding on the part of the reader of basic signal theory, including the time and frequency domains of signal analysis as implemented by modern audio and acoustic analyzers.
What Are They?
One way to understand FIR filters is to consider how they compare to their counterpart, the Infinite Impulse Response (IIR) filter. In general, IIRs are either analog, or they are digital filters that behave like analog filters. IIRs accomplish their response by using feedback (the good kind) to return some of the output signal back to the input for reprocessing. This “recursive” behavior means that in theory the filter’s impulse response (theoretically) never decays to zero. Of course, it does in a practical sense since the output signal eventually diminishes into the noise floor. Given their use of feedback, IIR filters can be unstable if not designed properly. Analog filters are IIR.
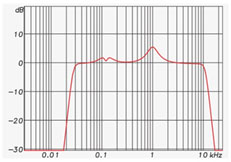
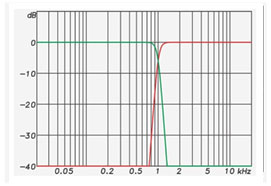
Let’s say we use an analog or IIR parametric equalizer to create a loudspeaker equalization curve (Figures 1 and 2). There is a high-pass response, a low-pass response, and some boost and cut filters within the passband.
Figure 1: The frequency response magnitude of an equalizer response.
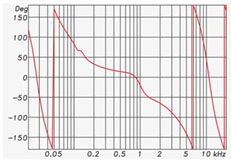
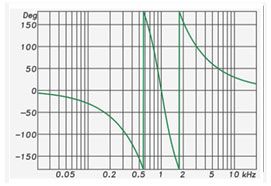
Figure 2: The frequency response phase of an equalizer response.
Each “bump” in the response exhibits a phase shift (negative-going phase angle) for those frequencies, and each “dip” exhibits the opposite phase shift (positive-going phase) for those frequencies. Both the high-pass and low-pass responses produce a negative-going phase angle with increasing frequency.
In other words, changes in the magnitude response are accompanied by shifts in the phase response. These phase shifts are unavoidable and inherent to the filter. In fact, they can often be predicted from looking at the magnitude response. When the magnitude and phase response are related in this predictable way, the relationship is called “minimum phase” and it is (sometimes) a desirable property of the filters.
Why? Because the bumps and dips in the loudspeaker’s frequency response are also (usually) minimum phase. This means that the equalizer fully “equalizes” the loudspeaker’s response, resulting in a smoother magnitude and phase response. So, in this context, “phase shift” is not an evil by product of using filters, as some might have you believe. As always, “it depends.”
To clarify, “minimum phase” does not mean the absence of phase shift. It means that the phase response exhibits the minimum possible shift for the given magnitude response, and that one can be predicted by the other. May measurement programs can calculate the minimum phase response, given the magnitude response.
Linear Phase
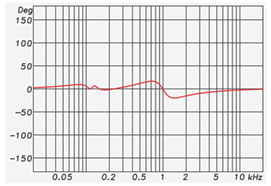
A FIR filter can have changes in its magnitude response that do not produce corresponding shifts in the phase response. Using the previous filter set, I replaced the HP and LP IIR filters with FIR filters of the same magnitude response.
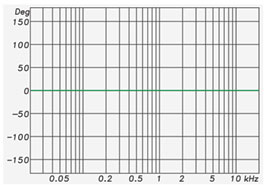
The phase response of such a filter is a straight line vs. frequency (linear frequency axis), so it is termed “linear phase.” Note that the phase shift due to the HP and LP have been removed, leaving only the phase shift produced by the boost and cut filters (Figure 3).
Figure 3: The use of FIR filters for the HP and LP.
So, for a minimum phase filter the magnitude and phase response are interdependent, and for an FIR filter they can be independent. FIR filters can change the magnitude response without changing the phase response.
For the remainder of this series, I will assume that IIR filters are minimum phase and that FIR filters can be linear phase. If exactly the same magnitude response curve were created with each, the phase responses could be different. In fact, if one looked only at the phase response of the HP and LP FIR filters in my example, they would have no idea that any filtering was going on.
Where FIRs really shine is when used for frequency dividing networks. The high-pass filter (HPF) used to protect a horn driver can be made arbitrarily steep using an FIR. Slopes of 96 dB/octave and higher can be realized.
A minimum phase filter (IIR or analog) with such a steep slope would have a horrific phase response, because when its magnitude response is steep, so is its phase response (refer again to Figure 2).
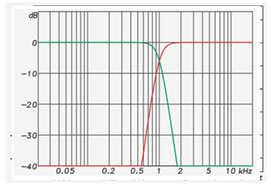
This puts a practical limit on the steepness (order) of IIR crossover networks due to the “time smear” caused by the filter. Figures 4and 5 show the magnitude and phase response of a 48 dB/octave Linkwitz-Riley IIR crossover network (HP and LP).
Figure 6 shows the magnitude response of an 8th order (96 dB/octave) FIR crossover network. Note that the filter slopes are much steeper than the IIR example. One would expect such aggressive changes to the magnitude response to be accompanied by very severe shifts to the phase response.
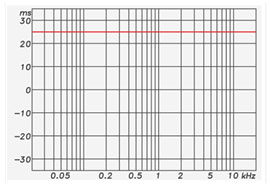
Figure 7 shows the group delay (GD) response of the summed filters, and Figure 8shows the phase response with the excess GD removed. Note that the phase response is linear.
With an FIR crossover network, I can have my cake and eat it too – “brickwall” rolloff characteristics and linear phase. That’s a big deal. Of course, I paid something for linear phase. This filter pair exhibits over 20 milliseconds of delay. Delay is one of the “push backs” that keep us from getting carried away with FIR filters.
Figure 4: The frequency response magnitude of a 48 dB/oct LR crossover. These filters sum to produce a perfectly flat magnitude response.
Figure 5: The frequency response phase of a 48 dB/oct LR crossover (filters summed).
Figure 6: The frequency response magnitude of a 96 dB/oct crossover network. These filters sum to produce a perfectly flat magnitude response.
Figure 7: The group delay response of the summed crossover filters.
Figure 8: The phase response with the group delay removed.
Two Types
Given the above, there are basically two types of filters used in audio work, each with multiple terms commonly used to describe them. They are:
There are obvious contradictions in these terms. For example, an IIR filter can be created in the digital domain. An FIR filter can be minimum phase. But, these are the “common usage” designators for the two filter types, useful for casual discussions. It is very important to clarify the terms when drilling down into the fine details. Which terms will I use in this article series? All of them, appropriate for the context in which they are used.
Impulse Response As A Filter
Those making loudspeaker and room measurements are familiar with the impulse response. It is measured by recording a Dirac pulse played through the system, although this technique is completely impractical for a number of reasons.
Most measurement systems acquire it by playing a log sine sweep, or “chirp” through the system, and capturing and processing the response into the IR.
The IR can be transformed to the frequency domain (Fast Fourier Transform or FFT), and displayed as a magnitude/phase plot. The magnitude/phase plot can be transformed (inverse Fast Fourier transform or iFFT) back to the time domain to be displayed as an impulse. As such, filters behavior can be described in either the time or frequency domains. If you’re using one of the garden variety dual-channel FFT measurement platforms, you’re already familiar with these concepts.
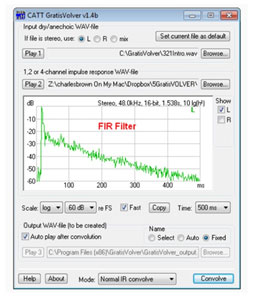
What’s this got to do with FIR filters? Impulse responses of loudspeakers and rooms are FIR filters, since they completely decay to zero (or noise) due to their finite length. Those who use GratisVolver to convolve room impulse responses (RIR) with anechoic program material are already working with FIR filters (Figure 9). For that reason, FIRs are sometimes called “time domain” or “convolution” filters, even though the actual implementation may be via multiplication in the frequency domain, carried out in software or hardware.
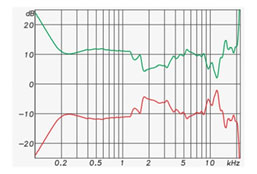
The IR of a loudspeaker can be transformed to the frequency domain and displayed as a frequency magnitude and phase. If inverted in the frequency domain (flipped upside-down), it is the exact conjugate (opposite) of the loudspeaker’s response in both magnitude and phase (Figure 10).
If the original and conjugate response are multiplied, they completely cancel each other, resulting in a flat line for the magnitude and phase (frequency domain) or a perfect impulse in the time domain.
Figure 9: GratisVolver convolves room impulse responses (FIR filters) with anechoic program material.
Figure 10: The frequency response magnitude of a 3-inch loudspeaker (red) and its conjugate response (green). If the green plot is used as an equalizer filter, the result is a perfect response. (Flat magnitude and linear phase in the frequency domain, and a perfect impulse in the time domain).
This has tremendous implications for equalization work – any measured response can be used as a filter. FIR “correction” filters can be used to:
- Make the loudspeaker’s response perfectly flat in magnitude and phase, even compensating for anomalies caused by throat reflections, grill effects and edge diffraction.
- Make corrections for room anomalies such as boundary effects near a loudspeaker, and (more in theory than practice) room reflections.
- Improve the response of line arrays by allowing individual processing for each array component. This can allow beam shaping and steering not possible with analog filters.
The FIR can be convolved with program material and used as a filter. While this has been possible for decades, it’s now becoming practical. Many DSPs are adding support for FIR filters, allowing an IR to be convolved in real-time with the program material passing through it.
But before you get too excited about have “perfect” loudspeaker responses, and cancelling room reflections, we have much more to discuss.
“Perfection” becomes possible through FIR filter equalization at a point in space. Since no two points in space have the same IR, we cannot extend the “correction” to an area. That doesn’t mean that FIR equalization is not useful, just that there are “push backs” that keep it from creating the perfect listening experience. We have to settle for some of the benefits under specific conditions that become increasingly difficult to realize as the room size increases.
Conclusion
Here are some take-aways from this introduction to FIR filters:
- The FIR can change the loudspeaker’s magnitude response without changing its phase response. This can allow very steep crossover filters that don’t introduce phase shift to the response. This linear phase behavior comes at the expense of latency.
- Any measured impulse response can be used as an FIR filter. This can allow us to listen to room data, such as with GratisVolver, or perform corrective equalization not possible otherwise. It can even be done on the fly, such as the echo cancellation utilized in conference room systems.
- FIRs can be implemented in software using convolution. An example is the use of GratisVolver to listen to room impulse response.
- FIRs can be implemented in hardware and used for real-time signal processing. Several DSPs now support user-specified FIR filters.
So, in the sound reinforcement world, FIRs are mostly about:
- Crossover networks.
- Corrective equalization for loudspeakers.
- Listening to room responses via convolution, whether measured or generated by a room modeling program.
- Beam forming in line array systems.
Audio filters are no longer just a collection of capacitors, inductors and resistors, or the equivalent realized through the use of integrated circuits. They can be produced by measurements or mathematical algorithms, and be implemented in real-time by advanced digital signal processing techniques.
In part 2, I’ll cover some more FIR filter basics, and show a couple of ways to produce “brickwall linear phase” FIR filters for a crossover network, including some measurements on real loudspeakers.